318. Биномиальные коэффициенты 1

Пусть n – целое неотрицательное число. Обозначим:

n! = 1 * 2 * ... * n (0! = 1),

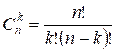
Для заданных n и k вычислите значение .

Вход. Первая строка содержит количество тестов t (t ≤ 50). Каждая из следующих t строк содержит два целых числа n и k (0 ≤ n < 2⁶⁴ и 0 ≤ < 2⁶⁴).

Выход. Выведите t строк, каждая из которых содержит значение для соответствующего теста.

Пример входа

Пример выхода

0 0

1 0

1 1

2 0

2 1

2 2

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Вычисления будем проводить с использованием 64-разрядных беззнаковых целых чисел (unsigned long long). Очевидно, что

= =

Присвоим переменной res значение 1, после чего будем ее умножать на для всех i от 1 до k. Каждый раз деление на i будет целочисленным, однако при умножении можно получить переполнение. Пусть d = НОД(res , i). Тогда операцию

res = res * (n – i + 1 ) / i

перепишем через

res = (res / d) * ((n – i + 1 ) / (i / d))

При такой реализации переполнения при умножении не произойдет (ответ является 64-разрядным беззнаковым целым числом). Заметим, что сначала следует выполнить деление (n – i + 1 ) / (i / d), а потом умножение res / d на полученное частное.

Для вычисления следует выполнить k итераций. Но что делать, если следует вычислить ? Ответ не превысит 2⁶⁴, поэтому такие входные данные возможны. Поскольку = , то при n – k < k следует положить k = n – k.

Пример

Рассмотрим следующий пример:

= =

Пусть res = 15, и осталось выполнить умножение res * = 15 *. Вычислим d = НОД(15 , 3) = 3. Поэтому 15 * = (15 / 3) * = 5 * = 20.

Реализация алгоритма

Функция gcd вычисляет наибольший общий делитель чисел a и b.

unsigned long long gcd(unsigned long long a, unsigned long long b)

{

return (!b) ? a : gcd(b,a % b);

}

Функция Cnk вычисляет значение биномиального коэффициента .

unsigned long long Cnk(unsigned long long n, unsigned long long k)

{

unsigned long long CnkRes = 1, t, i;

if (k > n - k) k = n - k;

for(i = 1; i <= k; i++)

{

t = gcd(CnkRes, i);

CnkRes = (CnkRes / t) * ((n - i + 1) / (i / t));

}

return CnkRes;

}

Основная часть программы. Читаем входные данные. Последовательно обрабатываем тесты.

scanf("%d",&t);

while(t--)

{

scanf("%llu %llu",&n,&k);

res = Cnk(n,k);

printf("%llu\n",res);

}

Java реализация

В Java отсутствуют unsigned типы, поэтому следует воспользоваться классом BigInteger.

import java.util.*;

import java.math.*;

public class Main

{

static BigInteger Cnk(BigInteger n, BigInteger k)

{

BigInteger ONE = BigInteger.ONE, CnkRes = ONE;

if (k.compareTo(n.subtract(k)) > 0) k = n.subtract(k);

for(BigInteger i = ONE; i.compareTo(k) <= 0; i = i.add(ONE))

CnkRes = CnkRes.multiply(n.subtract(i).add(ONE)).divide(i);

return CnkRes;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int tests = con.nextInt();

while(tests-- > 0)

{

BigInteger n = con.nextBigInteger();

BigInteger k = con.nextBigInteger();

BigInteger res = Cnk(n,k);

System.out.println(res);

}

Python реализация – comb

Для вычисления биномиального коэффициента воспользуемся встроенной функцией comb(n, k) = .

import math

Читаем количество тестов t.

t = int(input())

for _ in range(t):

Читаем входные данные текущего теста.

n, k = map(int, input().split())

Вычисляем и выводим ответ.

res = math.comb(n, k)

print(res)

Python реализация

Функция Cnk вычисляет значение биномиального коэффициента .

def Cnk(n, k):

res = 1

if k > n - k: k = n – k

for i in range(1, k + 1):

res = res * (n - i + 1) // i

return res